Fiducials are an attempt to localize a robot without any prior knowledge about location. They use unique images which are easily recognizable by a camera. The precise size and orientation of a fiducial tag in an image can uniquely localize a camera with respect to the tag. By measuring the location of the tag ahead of time, the location of the camera with respect to the global frame can be found.
Aruco is a standard for fiducial tags. There are many variants but generally look like this:
Ubiquity Robotic's module accurately finds aruco tags in camera images. It relies on a compressed image stream from the robot camera and the camera's specs published as well. aruco_detect publishes a number of outputs, but crucially it sends a geometry_msgs transform relating the fiducial to the camera on the topic /fiducial_transforms. This needs to be inverted to get the transform from camera to tag.
TF publishingThe transform from camera to fiducial can be combined with a transform between the map and fiducial to find the pose of the camera. This is best done using ROS's extensive tf tooling. Each fiducial location can be published as a static transform and a TransformListener can find the total transform from map to camera.
aruco_detect is brought up as part of the cr_ros bringup.launch file, but can be independently launched with roslaunch aruco_detect aruco_detect.launch if the proper topics are supplied in the launch file. takes the output of aruco_detect and publishes pose messages. It is in cr_ros and also in the bringup file. Static tf publishers are also needed for tag position. See "adding a new tag" below. One static publisher is needed to correct a 90 offset. This should relate the frame fiducial_camera to rotated_fiducial_camera with a transform of π/2 in the yaw (rosrun tf static_transform_publisher 0 0 0 1.57079632679 0 0 /fiducial_camera /rotated_fiducial_camera 100).
New tags can be placed on the map and published as static transforms from within the bringup.launch file. To find the x, y, and z position, use a tape measure.
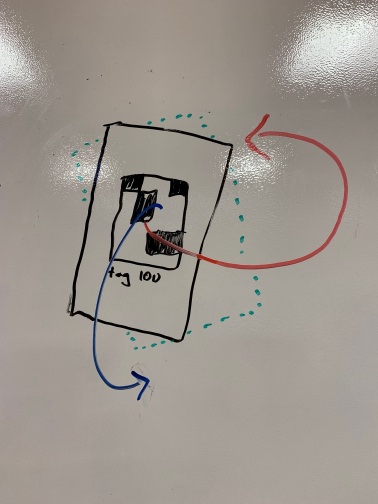
The three euler angles describing the angle of the tag are more difficult to determine. To find the first rotation parameter, x, consider the orientation of the fiducial relative to the map. If the fiducial faces north x = 0, if west x = π/2, if south x = π, if east x = 3π/2. The second (y) component accounts for leaning left or right of fiducial on the verical wall. If positioned straight up, it should be set to π which is approximately 3. The third (z) component describes how far forward or back the fiducial is oriented. If the wall is vertical, roll = 0. If leaning forward, 0 < z < π /2. If leaning backwards, 2π > z > 3π/2.
x is red, y is green, z is blue
Add a new tag to the bringup. The static publisher accepts x, y, z, for position and either yaw, pitch and roll or a quaternion for rotation, but for your own sake please chose the former.
Fiducials were very challenging to implement and it's worth spending some time discussing the reasons why and how we can learn from the process.
To start, fiducial localization involves complex coordinate transforms from image space to tag-relative space and then to map-relative space. By itself, this would have been fine. It is easy for a computer to calculate the matrix multiplication at the heart of these transforms, but it is hard for a developer to debug. More clarity and better documentation about the output of the tooling would have helped. In addition, the transforms are implemented in quaternions and other complex formats which are difficult to understand in any form and took some time to get used to.
A few tools exist which solve "fiducial slam" and originally we tried to implement one of those to compute the transforms from image space to map-relative space. These tools are, in fact, not built to solve that problem, but to assist in mapping the fiducials in the first place - a problem less challenging in our use case.
The biggest breakthrough came when I began using the built in tf tooling. This allowed me to work with a robust set of tools including rviz for easy debugging. Through this process I was able to see that the y and z axes needed to be swapped and that an inversion of the transform was needed. These were not clear when using other tools, but were at the heart of the strange results were were seeing early on.
More familiarity with ROS would have brought me to tfs sooner, but now I have that familiarity for next time. All together, I'm not sure what lesson there is to take away from this. Sometimes hardcore debugging is required.